Одна из распространенных задач на проценты — как изменилась цена товара, если ее сначала повысила на а%, а затем понизили на b%? Рассмотрим примеры решения таких задач.
Я предлагаю задачи такого вида разбивать на три части. Первую и вторую части удобно решать с помощью пропорции.
№ 1) Цену некоторого товара сначала повысили на 20%, а затем снизили на 25%. Как изменилась цена товара по сравнению с первоначальной?
Решение:
1) Обозначим, для определенности, первоначальную цену товара через m. Первоначальная цена в процентах — всегда 100%. Поскольку сначала цену повысили на 20%, то новая цена в процентах равна 100+20= 120%. Нам надо эту новую цену выразить через старую цену m, в рублях (или в других денежных единицах). Пусть х рублей- новая цена товара. Условие оформляем как при решении задач на проценты с помощью пропорции:
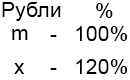
Составим пропорцию и решим ее:
![]()
![]()
![]()
Таким образом, после первого изменения новая цена товара стала равной 1,2m.
2) Переходим ко второму изменению цены. Теперь 100% — это 1,2m. Эту цену снизили на 25%, значит, новая цена 100-25=75%. Выразим новую цену через m. Пусть х рублей — новая цена товара.
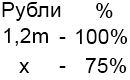
Составляем и решаем пропорцию:
![]()
![Rendered by QuickLaTeX.com \[x = \frac{{\mathop {1,2}\limits^{0,3} m \cdot \mathop {75}\limits^3 }}{{\mathop {100}\limits_4 }}\]](https://www.for6cl.uznateshe.ru/wp-content/ql-cache/quicklatex.com-754b52c6ab95f081caaff9a7a7229644_l3.png)
100 и 75 сокращаем на 25, 1,2 и 4 — на 4:
![]()
Таким образом, после второго изменения цена стала равной 0,9m.
3) Осталось выяснить, как изменилась цена по сравнению с первоначальной. Начальная цена m= 1∙m=100%m. Конечная цена 0,9m=90%m. Значит, цена уменьшилась на 100-90=10%.
Ответ: цена уменьшилась на 10%.
№2) Цену товара сначала понизили на 10%, а затем повысили на 10%. Как изменилась цена по сравнению с первоначальной?
Решение:
1) Обозначим первоначальную цену товара через m. Пусть х рублей — новая цена товара. Так как цену снизили на 10%, новая цена составляет 100-10=90% от старой.
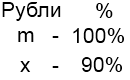
Составим и решим пропорцию:
![]()
![]()
![]()
2) Так как цену повысили на 10%, новая цена составляет 100+10=110% от старой. 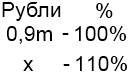
Составляем и решаем пропорцию:
![]()
![Rendered by QuickLaTeX.com \[x = \frac{{0,9m \cdot \mathop {110}\limits^{11} }}{{\mathop {100}\limits_{10} }}\]](https://www.for6cl.uznateshe.ru/wp-content/ql-cache/quicklatex.com-6d8a114dffc1eaa6c1424c7e4f2ea4b0_l3.png)
![]()
3) 0.99m=99%m. По сравнению с первоначальной новая цена уменьшилась на 100-99=1%.
Ответ: цена уменьшилась на 1%.
