Обратно пропорциональная зависимость

Две величины называются обратно пропорциональными, если при увеличении одной из них в несколько раз другая уменьшается во столько же раз. Соответственно, при уменьшении одной из них в несколько раз другая увеличивается во столько же раз.

Зависимость между такими величинами — обратно пропорциональная зависимость. Примеры обратной пропорциональной зависимости:

1)  время, затраченное на прохождение определенного пути, и скорость, с которой этот путь был пройден — обратно пропорциональные величины;

2) при одинаковой производительности труда количество рабочих, выполняющих определенную работу, обратно пропорционально  времени выполнения этой работы;

3) количество товара, купленного на определенную сумму денег,  обратно пропорционально его цене.

Чтобы отличить обратно пропорциональную зависимость от прямой, можно использовать пословицу: «Тише едешь — дальше будешь».

Задачи на обратно пропорциональные величины удобно решать с помощью пропорции.

Рассмотрим примеры задач на обратно пропорциональную зависимость.

1) 24 человека за 5 дней пропололи участок. За сколько дней выполнит ту же работу 30 человек, если будут работать с той же производительностью?

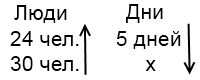
(Рассуждаем так:

1. В заполненном столбце стрелку ставим в направлении от большего числа к меньшему.

2. Чем больше людей, тем меньше времени нужно для выполнения определенной работы. Значит, это — обратно пропорциональная зависимость.

3. Поэтому вторая стрелка имеет противоположное направление).

Решение:

Пусть за х дней могут прополоть участок 30 человек. Составляем пропорцию (в направлении от начала стрелки к ее концу):

   

Чтобы найти неизвестный крайний член пропорции, надо произведение средних членов разделить на известный крайний член:

   

24 и 30  сокращаем на 6, 5 и 5 — на 5:

   

Значит, 30 человек выполнят эту работу за 4 дня.

Ответ: за 4 дня.

2) Для перевозки груза автомашине грузоподъемностью 7,5 тонн пришлось сделать 12 рейсов. Сколько рейсов понадобится сделать автомашине грузоподъемностью 9 тонн для перевозки этого же груза?

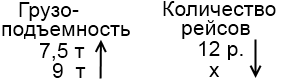
(1. В заполненном столбце ставим стрелку в направлении от большего числа к меньшему.

2. Чем больше грузоподъемность машины, тем меньше рейсов ей нужно сделать, чтобы перевезти груз. Значит, это — обратно пропорциональная зависимость.

3. Поэтому вторая стрелка имеет противоположное направление).

Решение:

Пусть х рейсов потребуется машине грузоподъемностью 9 тонн, чтобы перевезти груз. Составляем пропорцию (от начала стрелки к ее концу):

   

   

   

Значит, понадобится 10 рейсов.

Ответ: 10 рейсов.