Задачи на проценты | Математика для школьников

Удобнее всего решать задачи на проценты в 6 классе с помощью пропорций. Для составления пропорции нет необходимости выяснять вид задачи на проценты. Нахождение числа по его процентам, процентов от числа и процентного отношения чисел в этом случае проходит по одинаковой схеме, что существенно упрощает решение.

Задачи на проценты относятся к задачам на прямую пропорциональную зависимость, но при составления условия стрелки обычно не рисуют. Условие оформляется максимально просто: в первом столбце — единицы измерения, во втором — проценты.

Рассмотрим примеры задач на проценты, решаемые с помощью пропорции.

1) Сколько килограммов соли содержится в 40 кг 3-процентного раствора?

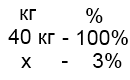
Решение:

Пусть х кг соли содержится в растворе. Составляем пропорцию:

$40:100 = x:3$

(Здесь пропорцию составили по строкам. Можно также составлять ее по столбцам, например, в направлении от большой величины — к меньшей: 40:х=100:3).

$x = \frac{{40 \cdot 3}}{{100}}$

$x = 1,2$

Значит, в растворе содержится 1,2 кг соли.

Ответ: 1,2 кг.

2) В саду растет 64 вишневых дерева, что составляет 16% всех деревьев. Сколько всего деревьев в саду?

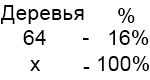Решение:

Пусть х деревьев всего в саду. Составляем пропорцию:

$64:16 = x:100$

$x = \frac{{\mathop {64}\limits^4 \cdot 100}}{{\mathop {16}\limits_1 }}$

$x = 400$

Значит, всего в саду 400 деревьев.

Ответ: 400 деревьев.

3) В книге 130 страниц. Саша прочитал 104 страницы. Сколько процентов книги прочитал Саша?

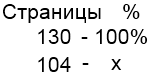Решение:

Пусть х% книги составляют прочитанные страницы. Составим и решим пропорцию:

$130:100 = 104:x$

$x = \frac{{\mathop {100}\limits^{10} \cdot \mathop {104}\limits^8 }}{{\mathop {130}\limits_{\mathop {13}\limits_1 } }}$

130 и 100 сокращаем на 10, затем 13 и 104 сокращаем на 13:

$x = 80$

Значит, Саша прочитал 80% книги.

Ответ: 80%.

В некоторых случаях задачи на проценты можно легко решать устно. Как это делается, я расскажу позже.

4 комментария к “Задачи на проценты”

Елена
17.04.2019 в 11:18

Уважаемая Светлана Михайловна! Не поможете решить задачу? В составе винограда 80% воды.В изюме — 15% воды.Сколько кг винограда надо взять, чтобы получить 400 гр.изюма?

Ответить
1. Светлана Михайловна
  18.04.2019 в 11:28
  
  Елена, постараюсь напрячься и сегодня написать отдельный пост о решении задач такого вида. Меня уже спрашивали, но, увы, так и не ответила ещё.
  
  Ответить
Максим
07.06.2019 в 06:38

Светлана Михайловна, можно за Вас?:)
В изюме и винограде количество мякоти одинаково, изменяется только количество воды.
Соответственно в изюме мякоти 85%, т.е. 400 * 0.85 = 340 гр. Эти же 340 гр. содержатся и винограде и составляют 100-80=20% от общей массы винограда. Поэтому 100% массы винограда = 340 * 5 = 1700 гр.

Ответить
1. Светлана Михайловна
  07.06.2019 в 17:55
  
  Конечно можно, Максим!
  Всё верно. Только я предпочитаю оформлять как две отдельные простенькие задачи и составлять пропорцию, но это уже дело вкуса)
  
  Ответить

4 комментария к “Задачи на проценты”

Оставьте комментарий Отменить ответ